e - the Most Important Number

There is a general fascination with π (pi) among people, with over 50+ quizzes on the digits of π on JetPunk for example. However, there is an equally important number, e, often omitted from the spotlight. By comparison, there are currently fewer than 10 quizzes here on digits of e.

One obvious reason why e is less popular than π is that π is a relatively simple concept that is learnt during primary school, and most people are quite familiar with it. On the other hand, students generally do not learn e until senior high school or even university. Many people would not know the significance of e and its application. So in this blog, I will try to briefly explain the number e and why you should know more about it (if you do not already).

I know that many readers here are still studying and may not understand complex mathematics. I try to keep things simple so that you do not need to know calculus to comprehend this blog. However, you do need to know some basic mathematics such as exponentials, roots, logarithms (a^b, √a, log a), and trigonometry (sine, cosine, radian), i.e. roughly junior high school level of maths depending on country.

Similar to π = 3.141592654... which is an irrational number with infinite number of non-repeating digits, e or the Euler's number is also an irrational number:

e = 2.718281828459045...

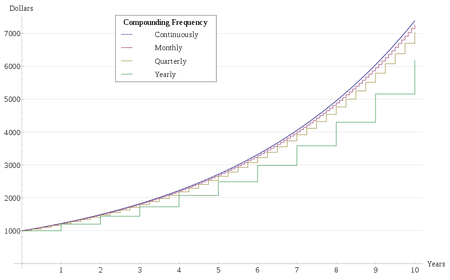
While π is to do with circle (circumference divided by diameter), e is related to exponential growth (or decline). Originally, e was discovered by asking the question on compound interest.

Let's say I borrow $100 at 10% interest per annum. If interest is calculated once a year, then after 1 year, I will be owing

$100 x (1 + 10%) = $110

And after 2 years,

$110 x (1 + 10%) = $100 x (1 + 10%)² = $121 etc.

But if interest is calculated monthly rather than yearly, then after one month, I will be owing

$100 x (1 + 10% / 12) = $100.83

$100.83 x (1 + 10% / 12) = $100 x (1 + 10% / 12)² = $101.67

and you can see that after 12 months, I will be owing

$100 x (1 + 10% / 12)¹² = $110.47

which is greater than $110 when interest is calculated yearly. This is because interest is compounded, i.e. interest charged in previous period is earning new interest in the next period.

However, if the bank is greedy, it can charge interest daily rather than monthly, which will become

$100 x (1 + 10% / 365)³⁶⁵ = $110.52

But why stop there? The bank can charge me interest every second, every millisecond until it is charged continuously. In such case, what is the maximum amount I'll be owing? If this is put into a formula, we are asking what the following answer would be if n becomes infinite.

(1 + 1 / n)ⁿ = ?

Let's say if you put n = 1,000,000 into the calculator, it would return 2.7182804691, which is very close to e. To put it in fancy mathematical notation:

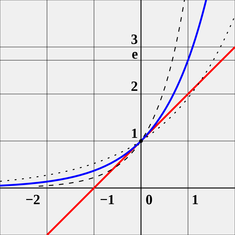
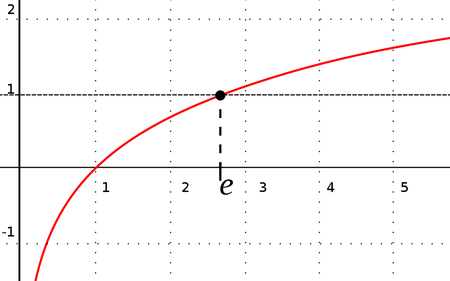
What makes e significant is its property of natural growth. If we put y = e^x on a chart, its rate of growth, i.e. the slope at any given point on the curve, equals to its value.

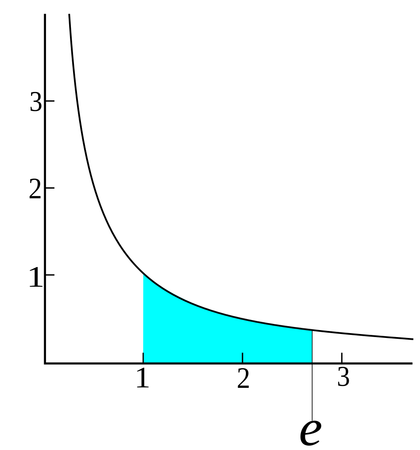
Reversely, the logarithm base e is called the natural log (or ln). Its chart (y = ln x) is the mirror image of y = e^x, and the area under the curve between 1 and e is exactly 1.

So does the area between 1 and e in the y = 1 / x graph (the hyperbola).

To explain these, you need to learn calculus.

Again, the proof requires understanding of calculus so I won't explain it here. If you put x = 1, e can also be described as

You can try this in a calculator and you can see that the value gets closer and closer to 2.71828...

We all know that the square of a number is always positive, because multiplying a negative number to another negative number results in a positive number. We all learnt this rule when we were kids and never question why. I am not going to explain it here but you can read this, which can hopefully convince you that mathematicians did not make up the rules to make lives harder.

Anyway, because of this, we know that √−1 is undefined. Try that in your calculator and the poor machine will return an error. But mathematicians made up an imaginary number i such that i² = -1.

They didn't do this just for fun though. Once we have the imaginary number i, things can get very interesting. For example, we know that -1 oscillates between 1 and -1 with its exponentials:

(-1)¹ = -1
(-1)² = 1
(-1)³ = -1
(-1)⁴ = 1

For i, it cycles between 1, i, -1 and -i

i⁰ = 1
i¹ = i
i² = -1
i³ = i² x i = -i
i⁴ = i² x i² = -1 x -1 = 1

To make things even more interesting, combining real and imaginary numbers become complex number z, in the form of:

z = a + bi

For example, 2 + 3i, 3 - 4i etc. Complex numbers can be plotted in an x-y chart called the Argand diagram, where the x-axis represents the real component and the y-axis the imaginary.

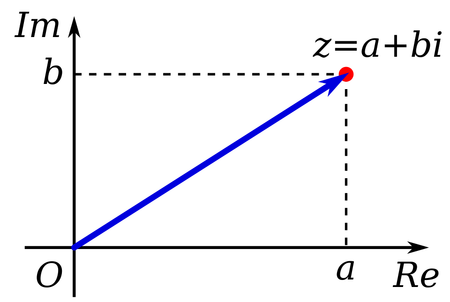
As such, instead of writing z = a + bi, it can be written using trigonometry:

z = r (cos θ + i sin θ)

where r (the radius) is called the modulus, and the angle θ is called the argument.

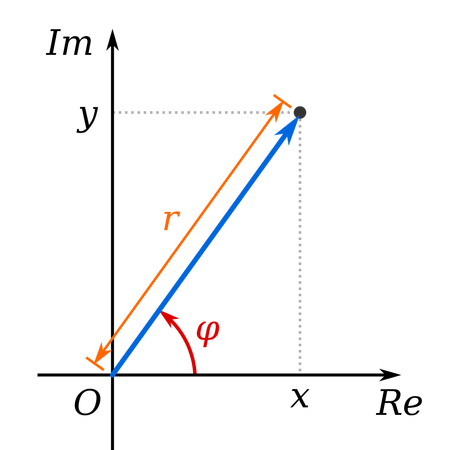
So why do I spend so much time explaining complex number when I am talking about e? It is because it can be easily proven that a complex number in polar or mod-arg form can be written as an exponential of e, i.e.

cos θ + i sin θ = e^iθ

This is the famous Euler's formula, named after Leonhard Euler, the genius Swiss mathematician in the 18^th century. I am not going to explain the proof here because (you guess what?) it needs some basic knowledge of calculus. If you are interested, you can find it easily in textbook or the internet.

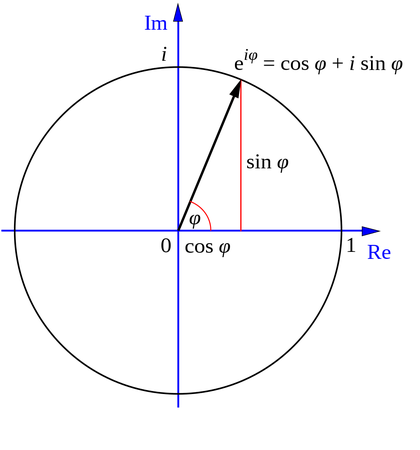
For any complex number with a modulus r = 1, it lies on the unit circle in the Argand diagram like the one above. This includes i at (0,1) coordinate, -1 at (-1,0) etc. For these numbers, their exponentials also lie on the unit circle at different angles. For example,

z² = (cos θ + i sin θ)²
    = (e^iθ)²
    = cos (2θ) + i sin (2θ)

that is, moving the point anticlockwise by doubling its angle. Similarly,

1/z = z^-1
      = cos (-θ) + i sin (-θ)
      = cos θ - i sin θ

which means flipping the point over the x-axis.

Another obvious derivation is when θ = π radian or 180 degree, which represents -1 + 0i = -1. It gives the famous Euler's identity

e^iπ + 1 = 0

This formula links nicely the five most important numbers in a single equation, namely 0, 1, e, π and i. This is widely admired by all mathematicians for its simplicity and beauty.

This blog is a very basic introduction on e. The number is also widely used in many other fields, such as applied statistics, number theory, electrical engineering etc. It is as important as π, and often regarded as a geek number, as demonstrated by the famous Google billboard in 2013.

The website, 7427466391.com (now defunct), led to a second more difficult question. By solving that, visitors would then be led to another webpage where they can submit their résumés to Google Labs.

And in 2014, Google announced its intention to raise US$2,718,281,828 in its IPO, which is e billion dollars rounded to the nearest dollar.

I hope that you now gain some appreciation of e and not overwhelmed by this mathematical blog. And finally, time to try the Digits of e quiz!