Some "Eurekas" of Mathematics - Part Two

Non-Euclidean Geometry

You measure the three interior angles of a triangle. You know they're going to add up to 180 degrees, right? No! All intuition from your high school geometry course may be triggered right now, but that's because when we think of geometry, unless you're a well-versed mathematician, we automatically jump to what's called the Euclidean plane, named after Greek "founder" of geometry Euclid. Euclid's axiomatic approach to geometry is more than likely the same way that you also learned (or will learn) geometry when you were (or will be) in a high school geometry course. This axiomatic approach takes a few basic statements, called axioms, as self-evidently true. You then use those axioms to prove other facts, then use those facts to prove more facts, and continue in this manner to discover more truths about geometry. This axiomatic approach is often used across mathematics as a whole.

So you may wonder, if we used Euclid's axioms to prove that the angles in a triangle must add up to 180 degrees, why did you tell me otherwise at the beginning of this blog? That is because there exist other "geometries" which begin with different axioms. That's why they're called non-Euclidean. So let's take a look at Euclid's axioms...

1. You can join any two points using exactly one straight line segment.
2. You can extend any line segment to an infinitely long line.
3. Given a point P and a distance r, you can draw a circle with center P and radius r.
4. All right angles are congruent.
5. If a straight line intersecting on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.

Each axiom seems pretty straight-forward and commonsensical, until we get to that fifth axiom. Even Euclid himself tried to keep it just to the first four axioms, but eventually realized the fifth axiom cannot be proved by the first four. So what exactly is that axiom saying? In the figure above, we see an example and counterexample. In the image, we see two lines with a straight line intersecting it. Notice how the two interior angles, α and β, do not together measure the same as two right angles (that is, 180 degrees). The fifth axiom says that since the sum of these two angles is not 180 degrees, then they must intersect. That is, they are not parallel. Often times this axiom is called the parallel postulate because it refers to when two lines are not parallel.

Now we can get to the fun part: non-Euclidean geometries. It wasn't until the 19th century that mathematicians realized that changing Euclid's fifth axiom creates entirely different "versions" of geometry.In one geometry, this fifth axiom is changed to

given a line and a point not on the line,
there exist at least two unique parallel lines through the point.

This is where our intuition tells us "no, that can't be possible!" The truth is that in our two-dimensional notion of geometry, no it isn't possible. But in a redefined hyperbolic geometry, it is. Consider the image below.

See how we have not 1, not 2, but 3 parallel lines through point p to our given line l. It's temping to say "but those lines aren't straight and they aren't extended infinitely." But in this geometry, using what appears to us to be a finite circle is actually an infinitely large plane. Take a look at the image below. Every triangle is the same size.

Another surface on which we can picture hyperbolic geometry is what's called the saddle-space (or just hyperbolic space). See the above picture. It's basically like an infinitely giant Pringle.

Now let's look at the other main non-Euclidean geometry. In this geometry, we modify Euclid's fifth axiom to say that

there are no parallel lines.

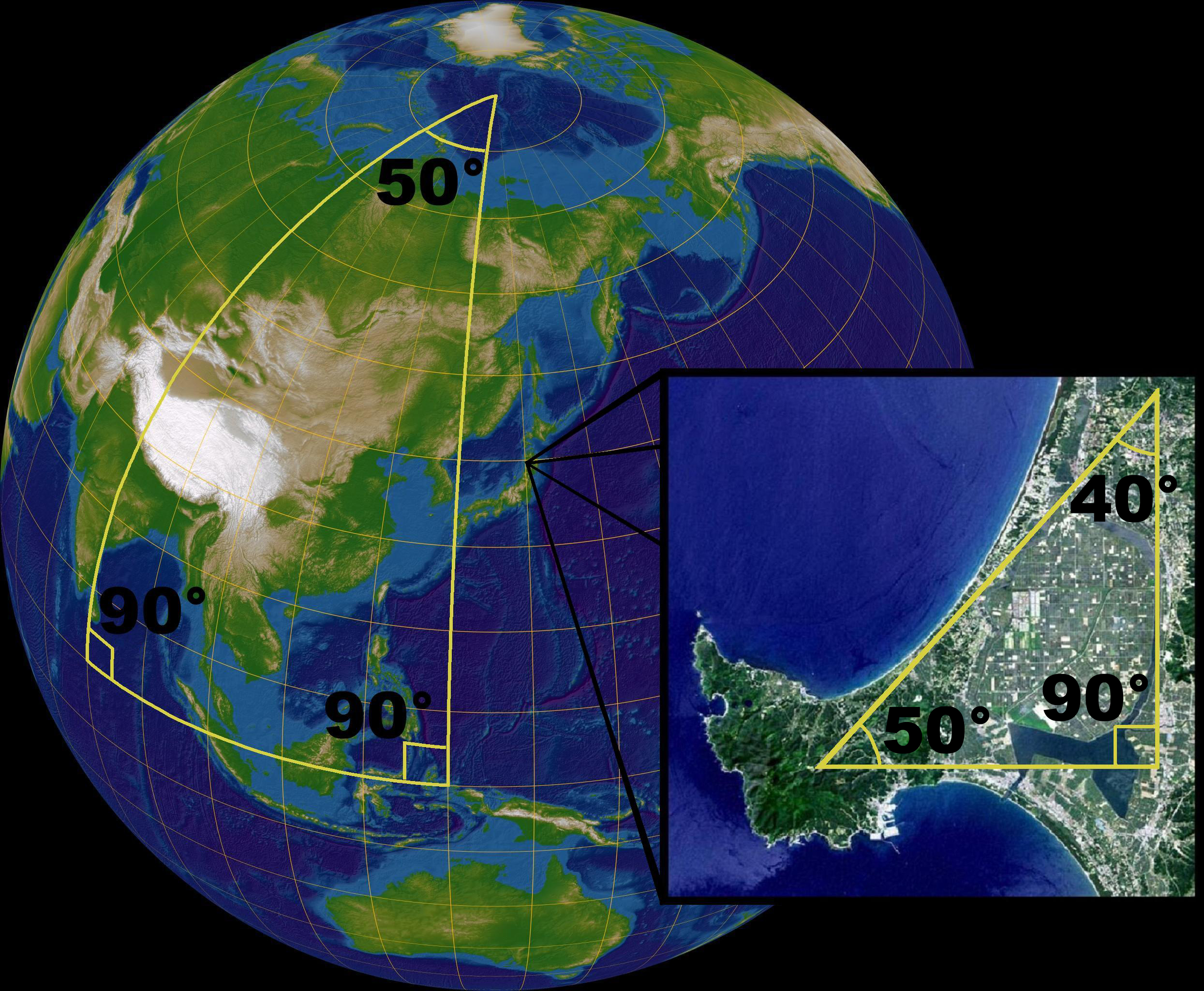
This is called elliptic, or spherical geometry. This is because in this geometry, the sphere can be use to represent the mathematical space.

So, now to our triangle whose interior angles add up to (strictly) greater than 180 degrees. Take a look at the following image, which depicts how a triangle in elliptic space may appear.

And since this is Jetpunk, I would be remiss to not apply this to geography. On a small scale, Euclidean Geometry is more practical and effective. Like if you're designing a garden or taking a look at a city map. But, on a bigger scale, spherical geometry is a much better representation. This is because the shortest path between two global cities isn't a straight line, but an arc along the Earth's surface.