Some "Eurekas" of Mathematics - Part Nine

I will be approaching the shuffling of cards by using something called group theory. If you're interested in mathematics, group theory is a great starting point for studying mathematics beyond calculus, statistics, and other high school level courses.

We will be looking only at the group S₅₂ which can be thought of as the various ways to rearrange the numbers 1 through 52. For example, one element in this group would switch the numbers 1 and 3 to give us the list: 3, 2, 1, 4, 5, 6, . . . , 50, 51, 52

Other elements in this group could switch more than just two numbers. For example, we could switch 1 and 2, then switch 2 and 3 afterwards.

The main point: group theory gives us a nice notation for symbolizing the various ways to rearrange a list of 52 items. And that's exactly what we do when we shuffle cards: we rearrange the order of 52 cards.

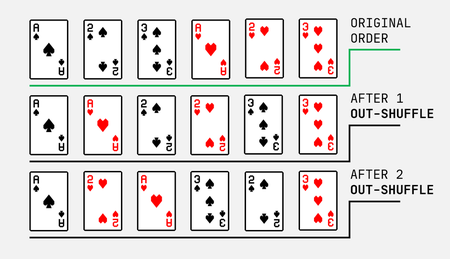
In this blog, we're just going to focus on "perfectly shuffling" cards. This means that you split the deck perfectly in half and alternate between the two separate piles, one at a time. But there are two types of perfect shuffles: the in-shuffle and the out-shuffle.

When performing the in-shuffle, after cutting the deck in half, you start the shuffle with the back half (cards in positions 27 through 52) of the deck. On the other hand, when performing an out-shuffle, you start the shuffle with the front half (cards in positions 1 through 26) of the deck.

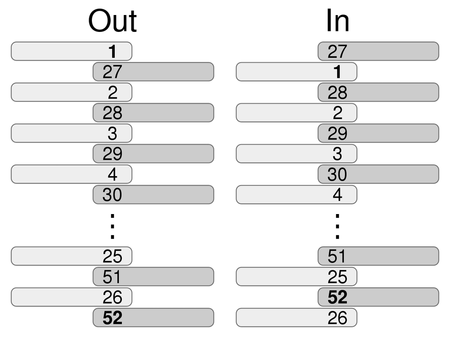
As you can see, in an out-shuffle, the first and 52st cards hold their position. However, in an in-shuffle, no card holds its position.

After performing an in-shuffle, the cards now take this order:

27, 1, 28, 2, 29, 3, 30, 4, 31, 5, 32, 6, 33, 7, 34, 8, 35, 9, 36, 10, 37, 11, 38, 12, 39, 13, 40, 14, 41, 15, 42, 16, 43, 17, 44, 18, 45, 19, 46, 20, 47, 21, 48, 22, 49, 23, 50, 24, 51, 25, 52, 26 

Let's try to represent what happens in an in-shuffle by using cycle notation, the conventional notation in group theory. To represent a permutation as such, you start with any number and write what position it moves to, you then write what position that second number takes on, and so on. Using this cycle notation, the shuffle will look like this:

(3 6 12 24 48 43 33 13 26 51 51 49 45 37 21 42 31 9 18 36 19 38 23 46 39 25 50 47 41 29 5 10 20 40 27 1 2 4 8 16 32 11 22 44 35 17 34 15 30 7 14 28)

This is because

- The number 3 moves to the 6th position,

- And the number 6 moves to the 12th position,

- And the number 12 moves to the 24th position, and so on.

We therefore can write a generic in-shuffle as a 52-cycle. It's a basic fact in group theory that if you repeat an n-cycle n times, you get back to the original configuration. So in this case, you would have to perform an in-shuffle 52 times in order to return to the original 1 through 52 configuration.

Now let's look at an in-shuffle, which will look much different. After performing an out-shuffle, the cards now take this order:

1, 27, 2, 28, 3, 29, 4, 30, 5, 31, 6, 32, 7, 33, 8, 34, 9, 35, 10, 36, 11, 37, 12, 38, 13, 39, 14, 40, 15, 41, 16, 42, 17, 43, 18, 44, 19, 45, 20, 46, 21, 47, 22, 48, 23, 49, 24, 50, 25, 51, 26, 52 

Using this cycle notation, we get something a bit different. This time the shuffle will look like this:

(1)(2 3 5 9 17 33 14 27)(4 7 13 25 49 46 40 28)(6 11 21 41 30 8 15 29)(10 19 37 22 43 34 16 31)
(12 23 45 38 24 47 42 32)(18 35)(20 39 26 51 50 48 44 36)(52)

This is because

- The number 1 is fixed in the 1st position,

- And then in the next cycle number 2 moves to the 3rd position,

- And the number 3 moves to the 5th position, and so on.

Now as opposed to the in-shuffle, we can write the out-shuffle as six 8-cycle, one 2-cycle, and two 1-cycles. This means that if you do the out-shuffle twice in a row, the 18th and 35th cards will return to their original position, because they make up the 2-cycle. Furthermore, if you do an out-shuffle any even number of times, the 18th and 35th cards will return to their original configuration.

This brings us to the interesting part of an out-shuffle. If you do it eight times, all the cards that comprise an 8-cycle will return to their original position. Furthermore, since eight is even, the cards in the 2-cycle will return to their position, and the 1st and 52nd cards never move. This means that if you perform a perfect out-shuffle eight times in a row, all the cards return to their original configuration.

So what, we should shuffle nine times? Counterintuitively, nine perfect out-shuffles is identical to just one out-shuffle. So this won't quite fix the issue. Luckily, you shouldn't have to worry about this since most likely you don't even split the deck perfectly in half when you shuffle. And even if you do perfectly cut the deck, you probably won't perfectly alternate cards from each pile. That being said, you should be fine shuffling as many times as you want, because with each error you make from doing a perfect shuffle, the greater the randomness you will likely end up getting.

I would recommend at least 3 or 4 random shuffles should do the trick. And if you're really paranoid about possibly being so perfect that you could perform eight out-shuffles in a row, just do an in-shuffle. You'd have to do fifty-two of those before your cards return to normal!

Another fun fact about mathematics & cards is that there are 52! different ways to arrange cards. That's 8x10⁶⁷, which is so big that if you threw a deck of cards on the ground right now and then picked them up in a random order, it's most probable that no deck of cards has ever been arranged in that order before.